En la clase del 26 septiembre comenzamos con un nuevo tema, el Dominio de Funciones. Este es un conjunto mayor de números reales, tales que el valor resultante f(x) es un numero real (conjunto de valores de x). En ocasiones no se especifica el dominio de una función, si no que la función aparece indicada por una ecuación en dos variables.
* En tales casos:
El Dominio de Función siempre sera igual a un numero real, por tal razón:
*No puede haber un 0 como denominador
*No puede haber un radical negativo
Ejemplos:
1) En esta gráfica el Dominio de Función seria negativo infinito e infinito ya que la recta se extiende infinitamente en ambas direcciones.
2) En este caso en el Dominio de Función X podría asumir cualquier numero entre negativo infinito e infinito.
3) Aquí se nos presenta una fracción, por lo tanto no puede haber un 0 como denominador.
Entonces: Que valores puede asumir X para que el denominador no sea 0?
La X asumir cualquier numero entre negativo infinito e infinito, con excepción de -3.
4) Aquí tenemos un radical y debido a que el Dominio de Funciones siempre dará a números reales, el radical no puede ser negativo.
Entonces: Que valor puede asumir X para que el radical no sea positivo?
X puede asumir cualquier numero que sea mayor o igual que -9.


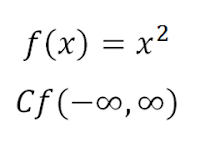


Este tema es bastante sencillo cn un poco de practica se puede realizar muy bien.
ResponderEliminarEste tema tambien al principio lo encontre un poco complicado por los radicales. Pero despues vi que no es nada del otro mundo y lo pude entender super bien.
ResponderEliminarPara mi este tema era el mas complicado en el examen, pero luego estudié y analizé los ejemplos y le pude encontrar la logica.
ResponderEliminarAdmito que este fue el tema mas frustrante. A la hora de estudiar para el examen, estaba totalmente perdida pero gracias a la practica y un poco de ayuda de mis companeros, pude analizar bien y darme cuenta que era mas facil de lo que parecia.
ResponderEliminarAl principio un poco perdida, pero luego de aclarar dudas, pude realizar los ejercicios con facilidad. Este es uno de los temas mas sencillos que hemos tocado, si nos ponemos a comparar.
ResponderEliminar